观历史中孕育文明的地域和城市，几乎都离不开河流和运输。无论是连通南北的京杭大运河，还是贯穿东西的丝绸之路，都是因为有了运输，物资和文明才得以交流、发展和繁荣。而反观我们熟悉的流体力学，也正是因为有了流体的输运，才有了速度、温度、压力以及各种组分和物理量的传递和变化，进而产生了丰富的流场结构。

大家都知道常见的流体输运方式有对流和扩散，那么它们是如何传输流体的？它们之间又有什么关系？我们还是从最基础的雷诺输运定理开始讲起。

01 雷诺输运定理

古希腊哲学家赫拉克利特曾经说过一句非常著名的话：“人不能两次踏进同一条河流”，这句充满哲理的话充分反映了运动是绝对的，静止是相对的。这句话对于河流和所有流体都适用，流体每时每刻都在运动，那么伴随着流体运动的物理量该如何去描述呢？这时候又要请出流体力学的大师雷诺同志了。

一般情况下，基本物理定理都是针对体系来描述的，但是流体运动太过复杂，难以定义体系的边界。通常分析流体运动多采用控制体法，而我们接下来介绍的雷诺输运定理就是把某个随流物理量的总和对时间的变化率以控制体的形式来表示。

在流场中任意取一控制体V，表面积为A。以t时刻位于控制体内的流体作为研究对象，此时，控制体与流体完全一致，占据下图中Ⅰ和Ⅱ的区域，∆t时刻后，流体运动到了新的Ⅱ和Ⅲ的区域，以N表示控制体内任意随流物理量（速度、能量、质量等），以η表示单位体积流体所具有的随流物理量。可以通过下图的方法推导出总的随流物理量对时间的变化率。

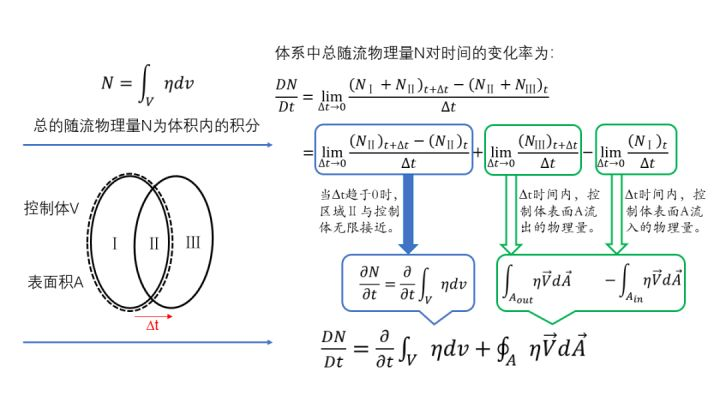
通过上述的推导，我们可以得到雷诺输运定理的数学表达式，同样可以得到它的物理描述：某时刻一个体系内的流体具有的总随流物理量对时间的变化率，等于该时刻控制体中总随流物理量对时间的变化率与单位时间内该物理量通过控制面的净流出之和。

注意等式的左侧为包含一团流体的体系，其体积和形状边界都随该部分流体的运动而变化，等式的右侧分别是针对静止控制体及其控制面的积分，被积函数也都是欧拉参考系中的变量。本质上讲，雷诺输运定理给出了一团流体的物理量变化在拉式坐标和欧式坐标下的转换关系。

没看懂？举个栗子吧。下午五点的时候，在卢比和钢蛋的小酒馆里面有100瓶冰镇啤酒， 1个小时后还有多少取决于两件事情：被顾客买走了多少和批发商送来了多少（通过控制面的变化），以及卢比和钢蛋偷喝了多少（控制体内的变化）。

02 流体输运的两种方式

雷诺输运定理在物理意义上和物质导数相同，实质上都是描述了流体的物理量伴随着流体而输运的含义。那么流体到底是怎么输运的呢？

流体的输运可以理解为一种流动的质量传递现象，主要包括对流和扩散两种方式。以下图中的火山爆发为例， 小伙伴们可以很容易的理解，火山喷发时从下向上的高速冲击便是对流，而喷出后的浓烟又会不断的向周围蔓延，便形成了扩散。

通过火山喷发的例子，小伙伴们可以看到，对流是依靠流体整体的运动传送物理量，可以理解为宏观上的机械运动，一般情况下，根据是否有外力作用可以分为强制对流和自然对流。

强制对流就是直接对流体施加压力或者刚体的转动和移动，强迫流体发生运动，比如在炎热的夏天，打开电风扇对着吹便是典型的强制对流。而自然对流则表示没有外力强制作用的情况下，由于温度等参数的不均匀而形成的密度差，从而导致重力场或其他力场中产生浮升力所引起的对流现象，比如一碗热气腾腾的牛肉面。

不同于对流是宏观的流体运动，扩散本质上是微观层面上，由分子热运动驱动的。理论上，分子热运动是随机的，但是当流场中的分子浓度或者热力学压力不均匀时，比如下图所示的流体两侧的分子浓度不同，那么显然，从左侧向右侧运动的分子数多于反向的，因此形成了从高浓度向低浓度扩散的现象，当然这也可以解释为粒子总是从高化学势向低化学势区域转移，直到两者相等并达到平衡。

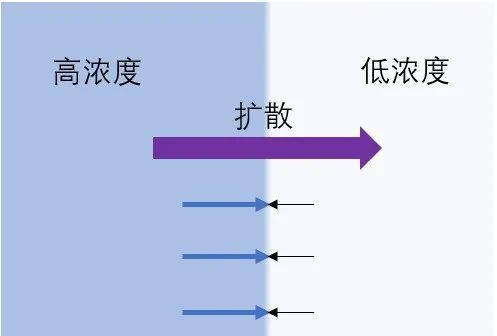
扩散是由无数单个粒子的随机速度引起的质量传递，而对流是由一团分子的平均速度引起的质量传递。一般而言，对流和扩散会同时出现在流场中，但是扩散会比强迫对流的速度慢很多，比如炒菜的时候产生的油烟，如果单纯的依靠扩散，则需要很长时间才能消散，如果打开抽油烟机，便可以通过强迫对流快速的将油烟排走。看来充分理解流体力学才能炒的一手好菜。

03 对流与扩散的秘密

流体的运动无时无刻不与对流和扩散发生着联系，而对流和扩散又常常同时存在，那么它们之间究竟是怎样的关系呢？

为了更好的描述流体输运过程中对流和扩散之间的关系，流体力学中将对流速率与扩散速率之比定义为一个无量纲数，命名为佩克莱数(Peclet number,简称Pe数），其中扩散速率是指在一定浓度梯度驱使下的扩散速率。在流动传质的情况下，Pe 数是雷诺数（Re）和施密特数（Sc）的乘积。而在流动传热中， Pe数相当于雷诺数（Re）和普朗特数（Pr）的乘积。

佩克莱数表征了对流和扩散的强度之比，而对流扩散方程则在数学上描述了对流扩散现象。如下图所示，对流扩散方程可拆解为对流方程和扩散方程，其中的φ为某一物理量，u代表了流动的速率，α代表了扩散速率。而对于传热问题，φ表示温度，α则表示热扩散系数，被输运的对象便是热量。

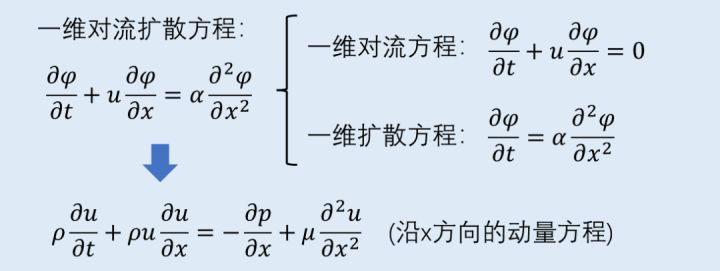
而如果把对流扩散方程中的α转化为粘度μ，并把被输运的物理量指定为动量，再加入压力的影响，那么一维对流扩散方程就变成了沿x方向上的动量方程。小伙伴们是不是感觉这个方程很眼熟？

没错，这就是忽略外力条件下的不可压缩N-S方程的一维形式。N-S方程可以理解为一个特殊的对流扩散方程，而此时流动所输运的恰恰是动量本身。而作为流体力学的葵花宝典，N-S方程中最痛的一刀就是方程的第二项，即速度输运速度自己。

04 无处不在的雷诺数

当然，对流和扩散还有另外一个小秘密。如果从时间的尺度研究对流和扩散，会得到更加有趣的关系。前面解释过，对流可以描述为流体的平均运动，因此对流的时间尺度可以描述为物理特征尺度和气流速度之比，而扩散的时间尺度则可以通过物理特征尺度和运动粘度来描述。假如我们把这两个时间相比，奇妙的事情便发生了，它们之间的比值恰恰是雷诺数Re的定义！

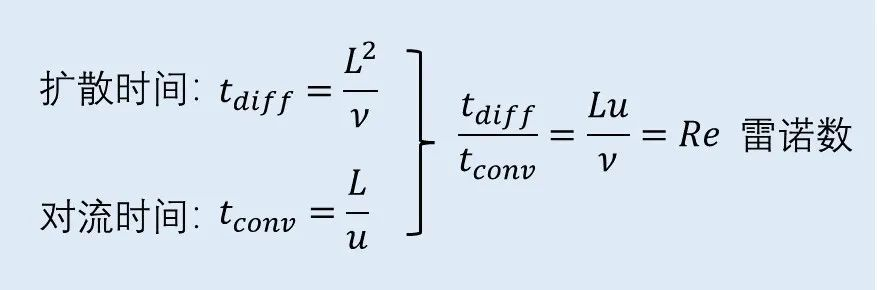
小伙伴们应该还记得雷诺数起源于经典的流动染色实验：当流体的物理尺度或流速增加，或流体的粘性减小时，流体的流态更趋向于某种混乱无规则的状态。

随后很长一段时间，众多学者沿着雷诺的足迹开始研究湍流的触发机理，却一直没有答案，直到1908年，恰逢第四届国际数学大会，索末菲将计就计，将他对流动稳定性和湍流触发机理的思考写成文章，并在历史上第一次明确以“雷诺数”命名这个神奇的无量纲数。

我们都知道雷诺数表示惯性力和粘性力的比值，当雷诺数很大时，则意味着粘性力对流动的影响很小，流体可以自由的流动，而当雷诺数很小时，则意味着粘性力占优。而从流体输运的角度出发，我们还能领会到扩散时间和对流时间的此消彼长。当雷诺数很大时，意味着扩散时间远远大于对流时间，对流的效应碾压了扩散，扩散也就渐渐被忽略了。

既然前面提到了流体力学中最重要的无量纲数Re和运动方程N-S方程，那么它们俩之间又要怎样的关系呢？公众号再次发扬“人狠话不多”的精神，直接推导不可压缩N-S方程的无量纲形式，如下图所示。

神奇的事情又一次发生了，无量纲的N-S方程只剩下一个无量纲数——雷诺数，它隐藏在扩散项中，这意味着雷诺数将很大程度上影响到无量纲N-S方程的解，当然这也从侧面反映了雷诺数对流动状态的影响。需要特别说明的是，上述推导仅适用于低速不可压的流动问题。对于高速问题，我们还需要考虑马赫数等无量纲数。

总结

对流和扩散就好像流体输运的一幅车轮，传输着流场中各种各样的物理量，也形成了形态各异的流场结构，它们携手从复杂的雷诺输运方程中走来，又一起回到了简洁的雷诺数，仿佛一个完美的流体力学闭环。

文章转载自LBM与流体力学